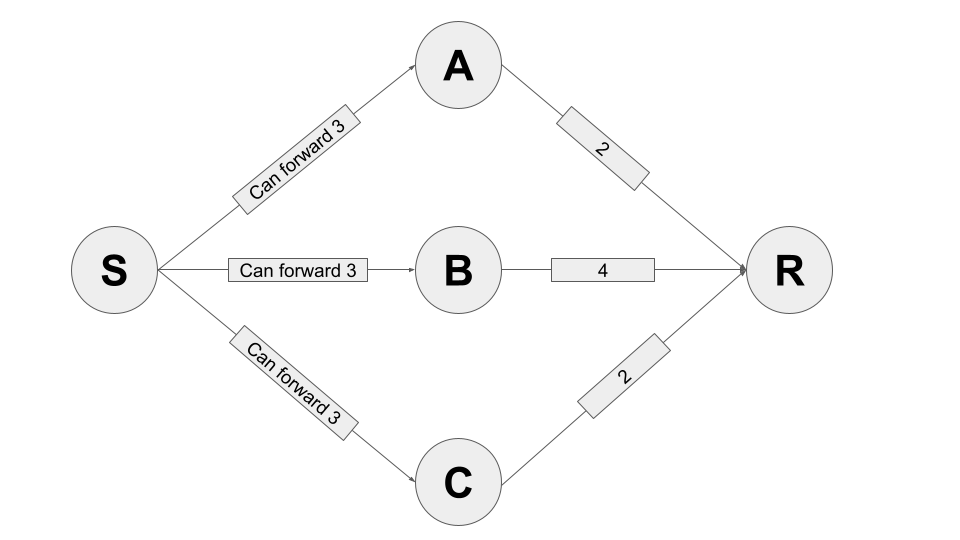
Mire el siguiente ejemplo de pink:
Asumir S quiere enviar 3 sábado R. Puedes asumir que S tiene suficiente liquidez en cada uno de sus canales locales para enviar a 3 Sats. También asuma la liquidez en los canales (A,R), (B,R) y (C,R) se distribuye uniformemente.
uno flujo de pago óptimamente confiable En este diagrama se ve así:
1 sat: S --> A --> R likelihood: 2/3
2 sats: S --> B --> R likelihood: 3/5
Este flujo tiene una probabilidad whole de 2/3*3/5 = 2/5 = 0.4 = 40%
La pregunta:
Cómo calcular el valor esperado de Satoshis para llegar a R si S envío 3?
Opción A
(Lo cual ya sé que está mal, pero lo escribo porque sospecho que algunas personas podrían tener un primer pensamiento comparable)
Inicialmente pensé que esto sería solo 3 sats * 2/5 = 6/5 sats = 1.2 sats que es lo que uno obtiene al multiplicar la cantidad a enviar con la probabilidad del flujo. Esto parece extraño ya que enviar 2 sats S-->B-->R tiene una probabilidad de 3/5 y con el razonamiento de un valor de expectativa de 2 sats * 3/5 = 6/5 sats = 1.2 sats. Como el valor esperado para 1 se sentó a lo largo del S-->A-->B el camino es más grande que 0 Esto sería una contradicción con la aditividad del valor esperado.
Opción B
A partir del razonamiento anterior, agregamos los valores esperados para las rutas disjuntas, así que:
E(3 sats) = 1 sat * 2/3 + 2 sat * 3/5 = 10/15 sats + 18/15 sats = 28/15 sats
Opción C
Por supuesto el camino 2 satoshi S-->B-->R no tiene que enviarse como una cebolla, pero podría enviarse como dos cebollas con 1 SAT cada una:
El primero tiene una probabilidad de 4/5 y el segundo tiene una probabilidad condicional de 3/4 que es extensamente explicado en este tema. Con la lógica de la opción B, uno debería poder agregar esos valores esperados. Por lo tanto, tenemos el valor esperado para enviar dos SAT en dos cebollas separadas de 1 S--> B --> R se calcularía como:
E(2 sats) = 1 sat * 4/5 + 1 sat * 3/4 = 31/20 sats
Si agregamos la cebolla de 1 sat de la S-->A-->R que period 2/3 sábado
esperaríamos tener
E(3 sats) = 31/20 sats + 2/3 sats = 93/60 sats + 40/60 sats = 132/60 sats = 33/15 sats
Esto es 5/15 sats = 1/3 sats más que la respuesta en la opción B
Opción D
Para empeorar las cosas, estoy confundido si los valores esperados de diseccionar la cebolla de 2 SAT en la opción C en dos cebollas de 1 SAT pueden sumarse linealmente, ya que la segunda cebolla está condicionada al tener 2 sats de liquidez en el canal. Si la primera cebolla ha fallado, la segunda ciertamente fallará. Por lo tanto, uno tendría que calcular el valor esperado para enviar dos cebollas de 1 SAT como esta:
E(2 sats) = 1 sat * 4/5 + 1 sat * 3/5 = 7/5 sats
Esto daría como resultado un valor whole esperado de:
E(3 sats) = 2/3 sats + 7/5 sats = 10/30 sats + 21/15 sats = 31/15 sats
Pensamientos
Solo para comparar aquí están los resultados
- Opción A:
18/15 - Opción B:
28/15 - Opción C:
33/15 - Opción D:
31/15
Si bien la opción B parece correcta, tiene sentido diseccionar aún más la cebolla de 2 sats. En las simulaciones que hice, parece que la opción D es correcta, lo cual es un poco sorprendente para mí. Usando el formalismo de la teoría de la probabilidad, la diferencia para el camino de 2 sat es:
- Opción C:
E(2 sats) = 1 sat * P(X>=1) + 1 sat * P(X>=2 | X >= 1) - Opción D:
E(2 sats) = 1 sat * P(X>=1) + 1 sat * P(X>=2)
Como se cube, la configuración simulada indica que la opción D es la respuesta correcta, pero eso es muy sorprendente para mí, ya que esperaría que el segundo término sea una probabilidad condicional.